Am Anfang des 20. Jahrhunderts von Mathematikern ersonnen, denen man besser nicht nachts im Park begegnen sollte
 Der "Sierpinski - Teppich".
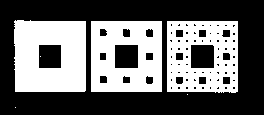
Der "Sierpinski - Teppich".
Man schneide aus einem Quadrat das mittlere Neuntel heraus. Die verbliebenen acht Quadrate unterziehe man dem selben Verfahren ... u.s.w. .. Man erhält ein Objekt mit einem Flächeninhalt gleich Null und einer unendlichen großen Kantenlänge.
 Der "Mengersche Schwamm"
Der "Mengersche Schwamm"
ist das dreidimensionale
Gegenstück zu obigem Perser - ein Monstrum von unendlichem Flächeninhalt und gleichsam nicht vorhandenem Volumen.
Wenn man viel Alkohol im Haus hat, lohnt es sich vielleicht darüber nachzudenken
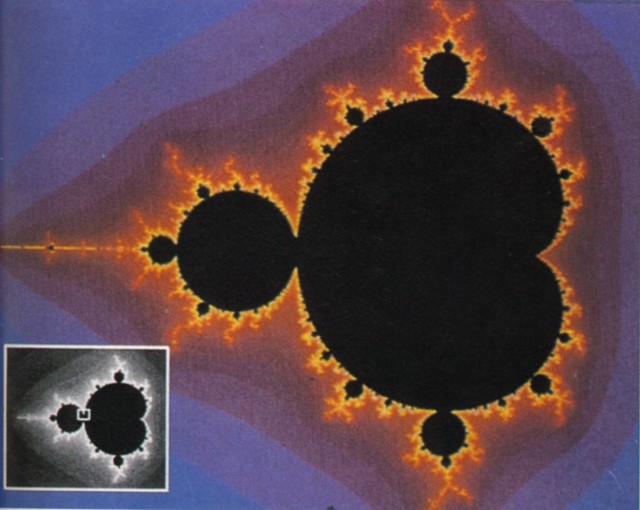

Das "Apfelmännchen" oder, was etwas bedeutsamer klingt,
die "Mandelbrodt - Menge"
Wieder springt uns die Selbstähnlichkeit förmlich an. Wieder ist ein Rückkopplungsprozeß die Grundlage und auch hier lassen sich Periodenverdopplungen finden.
Und nicht zuletzt finden wir auch
hier wieder ein Gebilde von bestechender Schönheit vor.
Das "Feigenbaum - Diagramm" und der Schock der Periodenverdopplung
"Die Ökologen waren in verschiedene Lager gespalten ... Die einen interpretierten die Botschaft, welche die Welt aussandte, als wohlgeordnet: Popultaionen verhielten sich regelmäßig und stetig - von
Ausnahmen abgesehen. Andere verstanden die Botschaft in genau entgegengesetztem Sinn: Populationen fluktuierten in erratischer Weise - von Ausnahmen abgesehen. Die Anhänger der These, Populationen verhielten sich regelmäßig, behaupteten,
sie würden durch deterministische Mechanismen geregelt. Diejenigen wiederum, die Populationen als erratische Phänomene betrachteten, hielten dagegen,Populationen würden von unberechenbaren Milieufaktoren manipuliert, so daß alle
deterministischen Einflüsse hinfällig würden.Entweder produzierte deterministische Mathematik stetiges Verhalten, oder zufällige äußere Störungen führten zu zufälligem Verhalten. Das war die Alternative.
In diese Debatte trug die
Chaosforschung eine erstaunliche Botschaft hinein: einfache deterministische Modelle konnten ein Phänomen hervorbringen, das wie zufälliges Verhalten anmutete."
... ein solches Modell vermittelt die sog. logistische Differenzengleichung:
xn+1 = r xn( 1 - xn )
- Sieht langweilig aus ... was macht man damit?
Diese Gleichung beschreibt einen Rückkopplungsprozeß. Jedes neue x ergibt sich aus dem alten x. Dabei bezeichnet n bzw. n+1 eine Art Zeitindex, dessen Wert die bereits vergangenen Tage oder Jahre beschreibt. n+1 ist der Index des neuen x-Wertes und n der des alten.
xn könnte z.B. die Zahl der Individuen eines Ökosystems am Tag n darstellen.
Man wählt also einen Startwert für x und untersucht, wie sich x verändert.
Es ergeben sich drei Varianten: x pendelt sich auf einen Wert ein, x pendelt sich auf mehrere Werte ein oder x fluktuiert ohne
ein erkennbares System. Welche der drei Möglichkeiten auftritt, hängt von dem Parameter r ab. Im nebenstehenden Diagramm ist das Verhalten des Rückkoppelungsprozesses in Abhängigkeit von r dargestellt - die Fragestellung lautet also:
wie verhält sich x in Abhängigkeit von r? Ab einem bestimmten r pendelt x zwischen zwei festen Werten - geht also von der Periode 1 zur Periode 2 über. Dies bezeichnet man als Periodenverdopplung. Diese Verdopplung setzt
sich fort, bis das System in chaotisches Verhalten übergeht.
x pendelt sich auf einen Wert ein, x pendelt sich auf mehrere Werte ein oder x fluktuiert ohne
ein erkennbares System. Welche der drei Möglichkeiten auftritt, hängt von dem Parameter r ab. Im nebenstehenden Diagramm ist das Verhalten des Rückkoppelungsprozesses in Abhängigkeit von r dargestellt - die Fragestellung lautet also:
wie verhält sich x in Abhängigkeit von r? Ab einem bestimmten r pendelt x zwischen zwei festen Werten - geht also von der Periode 1 zur Periode 2 über. Dies bezeichnet man als Periodenverdopplung. Diese Verdopplung setzt
sich fort, bis das System in chaotisches Verhalten übergeht. - Aha ... na und?
Jeder Lebensprozeß ist praktisch ein rückgekoppelter Prozeß, und man kann nur unter grober Vereinfachung Prozesse als nicht rückgekoppelt behandeln. Die oben beschriebene Rückkopplung war erstmals in der Lage, Populations - Entwicklungen besser zu beschreiben als die bisher benutzten mathematischen Modelle dies vermochten. Sie beschrieb sowohl regelmäßiges als auch chaotisches Verhalten. Das heißt nicht, daß sich Populationen tatsächlich genau so verhalten. Aber der Realität wurde wieder einmal ein Stück ihrer Unerfindlichkeit genommen.
Mehr zum Thema Was hat das alles mit Natur zu tun?:






