Man kann sich das hier alles durchlesen, wenn man an dem Modell der Simulation interessiert ist. Falls nicht, sind die Grafiken am Ende dieser Seite aber bestimmt einen Blick wert ...
Füchse (blau) und Mäuse (rot) krabbeln auf einem diskreten endlichen Universum
(x - y - Gitter) von Punkt zu Punkt. Füchse können Mäuse fressen und Mäuse
ernähren sich von "Pflanzen", an denen sie herumknabbern und die sich dann nach
und nach wieder regenerieren. Mäuse verhungern also, wenn sie nicht ihren
Aufenthaltsort ändern und zu neuen "Weiden" wandern. Ebenso verhungern Füchse,
wenn sie nicht durch das Universum streifen und so die Wahrscheinlichkeit
erhöhen, dass ihnen Mäuse über den Weg laufen, die sie fressen können.
Jedes Tier hat einen "Energievorrat", der durch Futter (Pflanzen bzw. Mäuse)
einen bestimmten Pegel nicht unterschreiten darf. Tritt dieser Fall trotzdem
ein, stirbt das Tier an Energiemangel - es verhungert.
Beide Spezies haben ein Lebensalter. Wird es überschritten, stribt das Tier.
Beide Spezies können Kinder in die Welt setzen. Allerdings nur auf Punkte des
Gitters in der direkten Nachbarschaft der "Mutter", die gerade unbesetzt sind.
Eine Population besteht jeweils aus der Menge "lebendiger" Mäuse und Füchse,
die jeweils von nur einer(!) bestimmten Spezies sind. Alle Füchse einer
Population haben also gleiche Eigenschaften. Gleiches gilt für die Mäuse.
Mäuse und Füchse können "sehen". Sie nehmen ihre direkte Nachbarschaft wahr und einen
Teil der etwas weiter entfernten Gitterpunkte. Entsprechend ihrer Umwelt
treffen Sie eine Entscheidung für ihren nächsten Aufenthaltsort. Wenn eine Maus
einen Fuchs wahrnimmt, flüchtet Sie, auch wenn Sie gerade hungert. Eine Maus läuft
vor einem Fuchs davon, indem Sie einen Sprung in die entgegengesetzte Richtung macht,
aus der der Fuchs kommt. Ist der Zielpunkt besetzt, ist dieser Bewegungsversuch
gescheitert und die Chancen für den Fuchs in die direkte Nachbarschaft der Maus
zu gelangen steigen. Hungert eine Maus, versucht sie sich zu einer Pflanze mit
höherem Energievorrat zu bewegen. Ist nichts Lohnendes für Mäuse und Füchse in
Reichweite, machen sie einen Schritt in eine zufällige Richtung - der Nase nach.
Frißt ein Fuchs eine Maus, erhält er deren Energievorrat, setzt aber eine Weile
(50 Tage) aus, um die Maus zu verdauem. Ein mißlungener Angriff kostet einen Fuchs
einen Teil seiner Energie.
Jede Bewegung und jeder Bewegungsversuch kostet Energie.
Nachkommen erzeugen kostet Energie und eine Ruhepause wird auch verordnet.
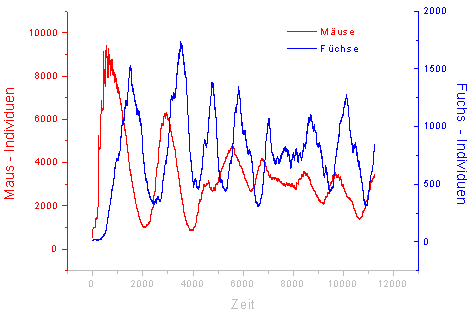
Ziel ist es, eine (quasi-) stabile Population zu erzeugen. Es muß also auf lange
Zeit hin ein dynamisches Gleichgewicht zwischen Füchsen und Mäusen entstehen.
Genauer gesagt sollte ein Räuber - Beute - Schema entstehen - idealer Weise derart,
daß sich die Anzahl von Mäusen und Füchsen ähnlich wie sin(x) und sin(x+pi/2) verhalten.
Die unabhängige Variable ist hier die Zeit, die in diskreten Schritten voranschreitet und
in diesem Text durch "Tage" umschrieben wird.
Stirbt eine Maus - oder Fuchs - Spezies aus, gilt der Versuch als gescheitert.
Das heißt, dass dieses Paar von Spezies nicht gemeinsam überlebensfähig ist. Die
Mäuse würden zwar ohne die Füchse prima zurecht kommen ... das ist aber nicht
der Sinn der Sache.
Die Eigenschaften einer Spezies sind durch einen Vektor an Parametern
festgelegt. Die Parameter bestimmen folgende Eigenschaften:
- Bewegungsgeschwindigkeit
- Höhe des maximal aufnehmbaren Energievorrates
- Energiewert, den jedes Tier an jedem Tag verbraucht
- Lebensalter
- mittlere Anzahl der Geburten - Tage pro Lebenszeit
- mittlere Anzahl der Nachkommen pro Geburten - Tag
Weitere nicht veränderbare Parameter bestimmen etwa das Sinken der Überlebenswahrscheinlichkeit, wenn das Individuum in die Nähe seines
Lebensalters gelangt.
Der Evolutions - Algorithmus:
Es liegen immer 10 Maus - Fuchs - Spezies - Paare vor, deren Tauglichkeit eine
stabile Population zu erzeugen getestet wird. Ein Maus - Fuchs - Spezies - Paar
(also zwei Parameter - Vektoren) ist im Evolutionsalgorithmus das Individuum. Die
Fitness - Funktion
für die Optimierung ergibt sich aus der Anzahl der Tage, die das
Individuum überlebt. Sterben alle 10 Individuen aus, erfolgt über Selektion,
Mutation und Rekombination der vorhandenen und bisher erfolglosen Individuen die
Erzeugung einer neuen Menge von 10 Individuen (also 10 Paare von Fuchs - Maus -
Spezies). Der Algorithmus ist also erfolgreich, wenn er "hängt", bzw. wenn die beiden
Spezies auf lange Sicht hin überleben.
Die Anfangs - Population wird per Zufall erzeugt. Dabei wird eine Anzahl von
Füchsen und Mäusen mit ebenfalls per Zufall ermittelten Lebensaltern in die Welt
gesetzt und anschließend aufeinander losgelassen.
Die Animationen sind graphische Darstellungen des Überlebenskampfes zweier Spezies im Zeitraffer.
Die Diagramme zeigen jeweils die zugerhörigen Populationsstärken der beiden Spezies über der Zeit. Dabei ist das erwartete (bzw. erhoffte) Räuber - Beute - Schema zumindest in der ersten Grafik eindeutig zu verzeichnen. In der zweiten Grafik ist das Schema in gezoomten Bereichen auffindbar.
Diese Darstellungen haben mit dem eigentliche Evolutionsalgorithmus nur sehr wenig zu tun, denn die eigentliche Aufgabe des Programmes ist es, zwei Arten (Fuchs und Maus) mit solchen Eigenschaften zu
finden, daß sich eine stabile Population entwickelt.
Aber schön bunt sind sie.